William Flannery earned his Ph.D. in engineering and went on to work on many significant projects in the aerospace industry such as the Galileo Space Probe, the Mars Observer, Space Station Freedom, and GPS systems. Engineering at this level is almost entirely based on calculus. Engineering analysis begins with the development of a differential equation model of the system to be studied. However, using traditional analytic calculus, differential equations are typically very difficult to solve. As a result, the study of differential equations is postponed until late in the calculus curriculum. Flannery realized that the world of calculus has changed drastically with the advent of computers, and that it no longer makes sense to avoid learning differential equations until many students have already given up on the study of higher math. Computational calculus makes this possible.
In Mathematical Modeling and Computational Calculus (MMCC), computational calculus doesn't use the formulas of analytic calculus. Instead it computes solutions to differential equations using very simple calculations based on the formula "distance equals velocity times time." Computational calculus requires lots of computations, so it was not practical before computers. Yet, Flannery says that as an engineer he used computational calculus almost exclusively.
He presents the following idea in his introduction: Newton developed calculus to solve the two-body problem, that is, calculating the trajectories of two bodies acted on by the force of gravity alone. The solution using analytic calculus is so difficult it is reserved for very advanced courses in mechanics. However it is easy to compute the trajectories using computational calculus by dividing the time interval into small subintervals and projecting the distance over each subinterval using the formula "distance equals velocity times time." It is the first system modeled and analyzed in MMCC. According to Flannery, computational calculus is this easy for every problem. I suspect the number of new concepts and the new vocabulary of math that need to be learned along the way make it a bit more challenging than Flannery claims. Nevertheless, this is a simpler approach.
Concepts are almost always taught within contexts such as rocket trajectories, electrical circuits, and automobile suspension systems. The projects in MMCC such as the calculation of the trajectory of the Juno space probe are beyond what you would normally expect. Juno was launched on August 5, 2011, and it follows a two year orbit around the sun and returns to earth where earth's gravity will "slingshot" it toward Jupiter. This is just one example of the two-body problem, and calculating the orbit is one of the exercises in MMCC. The result is shown by this diagram:
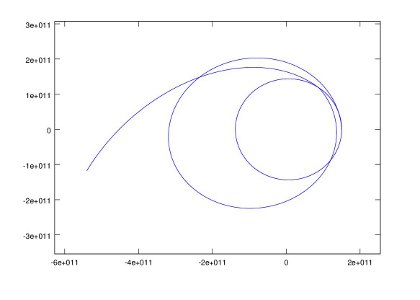
You can follow the progress of the real Juno probe here.
Concepts are practiced using paper and pencil and then implemented by a computer program written by the student that mimics the paper-and-pencil calculations but is capable of doing much more in a short time. For paper and pencil calculations, the book has a unique “checksum” self-checking feature. For these problems, there is a small square in the upper right corner of the problem with a number called “checksum.” Within the problem are lines for answers. Numbers entered on the solid lines for that problem are added together, and their sum should be equal to the checksum. There is also a free answer key online. (The link is at the very bottom of this web page.) Since there is no other form of accountability—no quizzes or tests—it does make it challenging for parents to ensure that students are actually checking and correcting their work. So Mathematical Modeling is most likely to work for self-motivated students who are really interested in learning.
Perhaps most important for many homeschooling families, MMCC does not require a teacher, although it is helpful if there is someone to consult if a student runs into a stumbling block. The course is best for students who have studied at least first year algebra and geometry, including some trigonometry. Students need not complete a precalculus course before tackling this course. With computational calculus there are no advanced calculations, just lots of relatively simple ones; the student does a few by hand then writes a computer program to automate the calculations he has already done by hand.
Flannery begins with basic functions and how we use them to represent motion in mathematical terms. The book moves at a slower pace through the first three chapters. Then there is an introduction to programming in MATLAB, a brief review of a few concepts in trigonometry, and the rest of the book focuses on modeling and applications and proceeds at a fairly rapid pace.
The course is taught in eight units:
- Constant Velocity Motion
- Mathematical Models of a Falling Object
- Graphing Solutions to Differential Equations
- Introduction to MATLAB/OCTAVE/FreeMat
- An Ounce of Trigonometry
- Orbits, Satellites, Rockets
- Electrical Circuits
- Dynamics
The unit titles give you at least a vague idea of what is covered. There are 10 to 16 lessons per unit. A lengthy synopsis with illustrations is available free on the website so you can really get an idea of how the course is taught. The synopsis proceeds chapter by chapter and presents many of the models used, the process of going from model to computation, and the programs that compute the solutions to three of the models.
This is serious calculus, but it’s presented with a more practical orientation rather than an emphasis on theoretical math. Students learn such things as how to compute the trajectory of a thrown object, the trajectory of a spring-box assembly, the trajectory of the Juno space probe, and the trajectory of tennis balls served with spin on the ball.
MATLAB is a programming language and a programming environment written for engineers that makes it very easy to automate simple calculations (as well as complex ones). While MATLAB is expensive, free systems that are MATLAB clones will work fine. Flannery recommends that students use FreeMat http://freemat.sourceforge.net/ which is a free environment for running MATLAB programs. You might have noticed that an entire unit helps students become familiar with the use of MATLAB and Freemat.
The spiral-bound book for this course is extra wide with 8.5 by 14 inch pages, and it is printed in black and white. Even though the cover image shown here is in color, the actual book cover is printed in black on colored card stock. The book comes with a money back guarantee and email support.
Students who will continue to study higher math will still need to take calculus or higher courses that teach the theoretical math, but this course might be the bridge that helps students become enthused enough about calculus to continue on to higher levels of math. It also might be a good course for those who want to understand what calculus is all about and how it is used even if they don’t intend to take any higher math courses.










